Hitunglah integral dari ∫_0^1▒ e^(2x+3) dx

Hitunglah integral dari ∫_0^1▒ e^(2x+3) dx

Jawab:

Misalkan:
u= 2x +3
dx = du/2

maka:
∫_0^1▒ e^(2x+3) dx = ∫_0^1▒ e^u du/2

=1/2 ∫_0^1▒e ^u du

=1/2 ( e^u |_0^1 )

=1/2 ( e^(2x+3) |_0^1 )

= 1/2 ( e^5-e^3 )

=1/2 e^3 ( e^2-1)

Tentukanlah integral dari ∫_1^5 |x-1|dx

Tentukanlah 

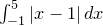
Jawab:

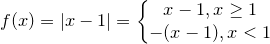
sehingga:

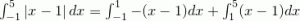
= -1/2 x^2+ x |_-1^1+1/2 x^2- x |_1^5

= [{-1/2 (1) + (1)} – {-1/2 (1) + (-1)}] + [{1/2 (25) – (5)} – {1/2 (1) – (1)}]

= – 1/2 + 1 + 0,5 + 1 + 12,5 – 5 –1/ 2 + 1

= 10

Tentukanlah ∫4^(x^2 ) xdx

Tentukanlah ∫4^(x^2 ) xdx

Jawab:

Misalkan:
u= x^2
dx = du/2x

Maka:
∫4^(x^2 ) xdx= ∫4^u x(du/2x)
=1/2 ∫4^u du

Karena : 4^u=e^uln4

maka:
=1/2 ∫e^uln4 du

Misalkan:
a = u ln 4
du = da/(ln 4)

Sehingga:
=1/2 ∫e^a (da/(ln 4))
= 1/(2 ln4) ∫e^a da
= e^a/(2 ln4)

Karena a = u ln 4 maka

= e^(u ln4)/(2 ln4)

Karena u= x^2 maka:

= e^(x^2 ln4)/(2 ln4)

Karena e^(x^2 ln4)=4^(x^2 ) maka

= 4^(x^2 )/(2 ln4)

Tentukan apakah turunan pertama dari y = |x+2| di x = -2 ada ?

Tentukan apakah turunan pertama dari y = |x+2| di x = -2 ada ?

Jawab:

syarat agar turunan pertama dari y = |x+2| di x= -2 ada adalah

turunan kiri = turunan kanan
f_(- )^’ (c)=f_+^’ (c)

maka :

f_(- )^’ (-2) = f_+^’ (-2)

-1 ≠ 1

Karena turunan kiri ≠ turunan kanan di x = -2
Maka turunan pertama dari y=|x+2| di x= -2 : Tidak ada

Tentukan Persamaan bidang singgung dari grafik eliptik paraboloid Z = x^3+x^3 y^3-2y^2 di titik (2,1,4).

Tentukan Persamaan bidang singgung dari grafik eliptik paraboloid
Z = x^3+x^3 y^3-2y^2 di titik (2,1,4).

Jawab:

Persamaan bidang singgung grafik z = f(x,y) di titik P(x_0,y_(0,) z_0) adalah

Z = z_0+ f_x(x_0,y_0) (x-x_0 )+f_y(x_0,y_0) (y-y_0 )

Maka:
f_x(x_0,y_0)=3x^2+3x^2 y^3
f_x(1,1)=12+ 12 = 24

Dan
f_y(x_0,y_0)=3y^2 x^3-4y
f_y(1,1)=24-4=20

Sehingga: Persamaan bidang singgung grafik Z = 2x^2+y^2 di titik (2,1,4) adalah

Z = z_0+ f_x(x_0,y_0) (x-x_0 )+f_y(x_0,y_0) (y-y_0 )

Z = 4+ 24 (x-2)+20 (y-1)

Z = 4+24x-48+20y-20

Z = 24 x+20y-64